Wiskunde speelt een doorslaggevende rol om het gedrag en de werking van te begrijpen elektrisch en elektronische systemen Veeltermen, algebra, waarschijnlijkheid, integraties en differentiaties enz… vormen een belangrijk onderdeel van de tools die worden gebruikt om de systemen op te lossen. Met de toenemende complexiteit van systemen zijn zeer geavanceerde methoden vereist. Differentiaalvergelijkingen worden prominent gebruikt voor het definiëren van besturingssystemen. Deze vergelijkingen zijn eenvoudig op te lossen. Maar complexiteit ontstaat bij het oplossen van differentiaalvergelijkingen van hogere orde. Om dergelijke complexe differentiaalvergelijkingen van hogere orde op te lossen, is de wiskundige methode die effectief bleek te zijn Laplace-transformatie Aangezien deze transformatie veel wordt toegepast, is het handig om te weten waarvoor ze echt bedoeld waren en hoe ze werken.
Wat is een Laplace-transformatie?
In de wiskunde worden transformaties toegepast om een variabele van de ene vorm naar de andere te transformeren om de vergelijking gemakkelijk hanteerbaar te maken. Laplace-transformaties doet vrijwel hetzelfde. Ze zetten differentiaalvergelijkingen van hogere orde om in een polynoomvorm die veel gemakkelijker is dan het rechtstreeks oplossen van differentiaalvergelijkingen.
Maar er zijn verschillende transformaties zoals Fourier-transformatie, z-transformaties, wat maakt Laplace-transformatie speciaal? Het grote voordeel van Laplace-transformatie is dat ze worden gedefinieerd voor zowel stabiele als onstabiele systemen, terwijl Fourier-transformaties alleen worden gedefinieerd voor stabiele systemen.
Laplace-transformatieformule
Een Laplace-transformatie van functie f (t) in een tijdsdomein, waarbij t het reële getal groter dan of gelijk aan nul is, wordt gegeven als F (s), waarbij er  s is het complexe getal in frequentiedomein .i.e. s = σ + jω
s is het complexe getal in frequentiedomein .i.e. s = σ + jω
De bovenstaande vergelijking wordt beschouwd als eenzijdig Laplace-transformatievergelijking Wanneer de limieten worden uitgebreid tot de gehele reële as, dan is de Bilaterale Laplace-transformatie kan worden gedefinieerd als
 In praktische circuits zoals RC- en RL-circuits meestal worden beginvoorwaarden gebruikt, dus eenzijdige Laplace-transformaties worden toegepast voor analysedoeleinden.
In praktische circuits zoals RC- en RL-circuits meestal worden beginvoorwaarden gebruikt, dus eenzijdige Laplace-transformaties worden toegepast voor analysedoeleinden.
Zoals s = σ + jω, gedraagt σ = 0 Laplace-transformaties zich als Fourier-transformatie.

Laplace-transformatieformules
Voorwaarden voor toepasbaarheid van Laplace Transform
Laplace-transformaties worden integrale transformaties genoemd, dus er zijn noodzakelijke voorwaarden voor convergentie van deze transformaties.
 d.w.z. f moet lokaal integreerbaar zijn voor het interval [0, ∞) en afhankelijk van of σ positief of negatief is, kan e ^ (- σt) vervallen of groeien. Voor bilaterale Laplace-transformaties in plaats van een enkele waarde convergeert de integraal over een bepaald bereik van waarden dat bekend staat als Region of Convergence.
d.w.z. f moet lokaal integreerbaar zijn voor het interval [0, ∞) en afhankelijk van of σ positief of negatief is, kan e ^ (- σt) vervallen of groeien. Voor bilaterale Laplace-transformaties in plaats van een enkele waarde convergeert de integraal over een bepaald bereik van waarden dat bekend staat als Region of Convergence.
Eigenschappen van Laplace Transform:
Lineariteit

Lineariteit
Tijdverschuiving

Tijdverschuiving
Verschuiving in S-domein

Verschuiving in S-domein
Tijdomkering

Tijdomkering
Differentiatie in S-domein

Differentiatie in S-domein
Convolutie in de tijd

Convolutie in de tijd
Initiële waardestelling
De beginwaardestelling wordt toegepast wanneer in Laplace-transformatie de graad van de teller kleiner is dan de graad van de noemer  Eindwaardestelling:
Eindwaardestelling:
Als alle polen van sF ('s) in de linker helft van de S-vlak eindwaarde stelling liggen wordt toegepast.
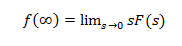 Inverse Laplace-transformatie
Inverse Laplace-transformatie
Vanwege convergentiekarakteristiek heeft Laplace-transformatie ook een inverse transformatie. Laplace-transformaties vertonen een-op-een-mapping van de ene functieruimte naar de andere. De formule voor Inverse Laplace-transformatie is
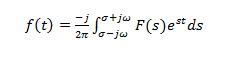 Hoe Laplace-transformatie te berekenen?
Hoe Laplace-transformatie te berekenen?
Laplace-transformatie maakt de vergelijkingen eenvoudiger te hanteren. Wanneer een differentiaalvergelijking van hogere orde wordt gegeven, wordt er Laplace-transformatie op toegepast die de vergelijking omzet in een algebraïsche vergelijking, waardoor deze gemakkelijker te hanteren wordt. Vervolgens berekenen we de wortels door deze algebraïsche vergelijking te vereenvoudigen. Nu wordt een omgekeerde Laplace-transformatie van een eenvoudigere uitdrukking gevonden die de gegeven differentiaalvergelijking van hogere orde oplost.

Laplace-transformatieberekening
Toepassingen van Laplace Transform
- Analyse van elektrische en elektronische schakelingen
- Complexe differentiaalvergelijkingen opsplitsen in eenvoudigere polynoomvormen.
- Laplace-transformatie geeft informatie over zowel stabiele als tijdelijke toestanden.
- Bij machine learning wordt de Laplace-transformatie gebruikt voor het maken van voorspellingen en het maken van analyses in datamining.
- Laplace-transformatie vereenvoudigt berekeningen in systeemmodellering.
Toepassing van Laplace-transformatie in signaalverwerking
Laplace-transformaties worden vaak gekozen voor signaalverwerking. Samen met de Fourier-transformatie, de Laplace-transformatie wordt gebruikt om signalen in het frequentiedomein te bestuderen. Als er kleine frequenties in het signaal in het frequentiedomein zijn, kan men verwachten dat het signaal vloeiend is in het tijdsdomein. Het filteren van een signaal gebeurt meestal in het frequentiedomein waarvoor Laplace fungeert als een belangrijk hulpmiddel voor het omzetten van een signaal van tijddomein naar frequentiedomein.
Toepassing van Laplace Transform In Control Systems
Besturingssystemen zijn meestal ontworpen om het gedrag van andere apparaten te regelen. Voorbeeld van controlesystemen kan variëren van een eenvoudige verwarmingsregelaar voor thuis tot een industrieel regelsysteem dat het gedrag van machines regelt.
Over het algemeen gebruiken regeltechnici differentiaalvergelijkingen om het gedrag van verschillende functionele blokken met gesloten lus te beschrijven. Laplace-transformatie wordt hier gebruikt om deze vergelijkingen op te lossen zonder verlies van cruciale variabele informatie.
Karakterisering van lineaire tijdinvariante systemen met behulp van Laplace-transformatie
Voor een losse systeem-ROC die aan het systeem is gekoppeld, is de functie het rechterhalfvlak. Een systeem is anti-casual als de impulsresponsie h (t) = 0 voor t> 0.
Als ROC van de systeemfuncties H (s) de jω-as bevat, dan is de L.T.I. het systeem wordt een stabiel systeem genoemd. Als een toevallig systeem met rationele systeemfuncties H (s) negatieve reële delen heeft voor al zijn polen, dan is het systeem stabiel.
Laplace-transformatie is dus een cruciaal hulpmiddel bij het analyseren van circuits. We kunnen zeggen dat een stethoscoop voor dokter Laplace transformaties zijn om ingenieur te controleren. Hoe beschouw je Laplace-transformaties als? Op welke manier waren ze nuttig voor u?
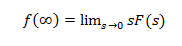 Inverse Laplace-transformatie
Inverse Laplace-transformatie 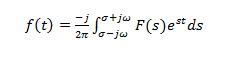 Hoe Laplace-transformatie te berekenen?
Hoe Laplace-transformatie te berekenen? 




![4 Simple Clap Switch Circuits [getest]](https://electronics.jf-parede.pt/img/4017-ic-circuits/21/4-simple-clap-switch-circuits.png)